题目描述

There is a non-transparent obstacle and a single-sided mirror in an infinite two-dimensional plane. The obstacle can be represented as a triangle and the mirror can be represented as a $\textbf{directional}$ line segment pointing from $(x_{m,1}, y_{m,1})$ to $(x_{m,2}, y_{m,2})$, with the right side being reflective.

There are $m$ stones at point $(x_1,y_1)$ and DreamGrid would like to move all the stones to point $(x_2,y_2)$. The following constraints must be satisfied:

• DreamGrid can only carry one stone each time.
• Once DreamGrid picks up a stone, he can only put it down at point $(x_2,y_2)$.
• Let $L$ be the path DreamGrid walked, then for each point $p$ on $L$, DreamGrid should see all the stones directly or through the mirror.

Note that:

• If some part of the line vision is inside the obstacle (it's ok that the line vision passes a point or edge of the obstacle), it's considered, that DreamGrid cannot see the stone with this line of vision.
• If one of the two endpoints of the mirror is on the line of vision, it's considered, that DreamGrid can see the stone both in the mirror and through the mirror.
• The reflection process is governed by laws of physics --- the angle of incidence is equal to the angle of reflection. The incident ray is in the same half-plane as the reflected ray, relative to the mirror.
• If the line of vision is parallel to the mirror, reflection doesn't take place, and the mirror isn't regarded as an obstacle.
• DreamGrid cannot move into the obstacle but can move on the edges or the vertices of the obstacle.
• DreamGrid cannot move through the mirror but can move on the mirror. Note that if DreamGrid is on the line segment of the mirror other than the two endpoints, he can only see the side he comes from, and cannot see through the mirror.

DreamGrid would like to know the shortest distance to move all stones from $(x_1,y_1)$ to $(x_2, y_2)$.

输入格式

There are multiple test cases. The first line of input is an integer $T$ (about 100), indicates the number of test cases. For each test case:

The first line contains one integer $m$ ($1 \le m \le 10^6$), indicating the number of stones.

The second line contains four integers $x_1$, $y_1$, $x_2$ and $y_2$, indicating the start point and the target point.

The third line contains four integers $x_{m,1}$, $y_{m,1}$, $x_{m,2}$ and $y_{m,2}$, indicating the coordinates of the mirror.

Each of the next $3$ lines has two integers $x_i$ and $y_i$, indicating the coordinates of the vertices of the obstacle.

All the coordinates will not exceed $100$ in absolute value. Both the start point and target point are outside the obstacle and the mirror. The mirror and the obstacle have no points in common.

It is guaranteed that no three points are collinear.

输出格式

For each test case, output a real number indicating the shortest distance, or output $-1$ if DreamGrid cannot move all the stones under the constraints.

Your answer will be considered correct if and only if the absolute error or relative error of your answer is less than $10^{-6}$.

2
2
-2 0 2 0
-3 3 3 3
0 1
-3 -2
3 -2
2
-2 0 2 0
-3 3 -1 3
0 1
-3 -2
3 -2

13.416407864999
-1

提示

We now welcome our special guest Mashiro, who heartily donates this problem to our problemset, to explain the sample test cases for us using her sketch book.

$\textit{(Image from pixiv. ID: 32084305)}$

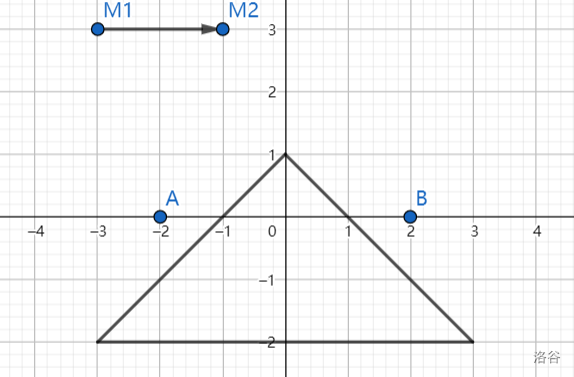
In the figures above, we indicate the start point as point $A$ and the target point as point $B$. The mirror is indicated by the line segment pointing from $M1$ to $M2$, with the right side being reflective.

For the first sample test case, the optimal path is $A \to C \to B \to C \to A \to C \to B$.

For the second sample test case, as DreamGrid cannot see $A$ from $B$, it's impossible to move all the two stones from $A$ to $B$ while following the constraints in the problem description.